Text diff

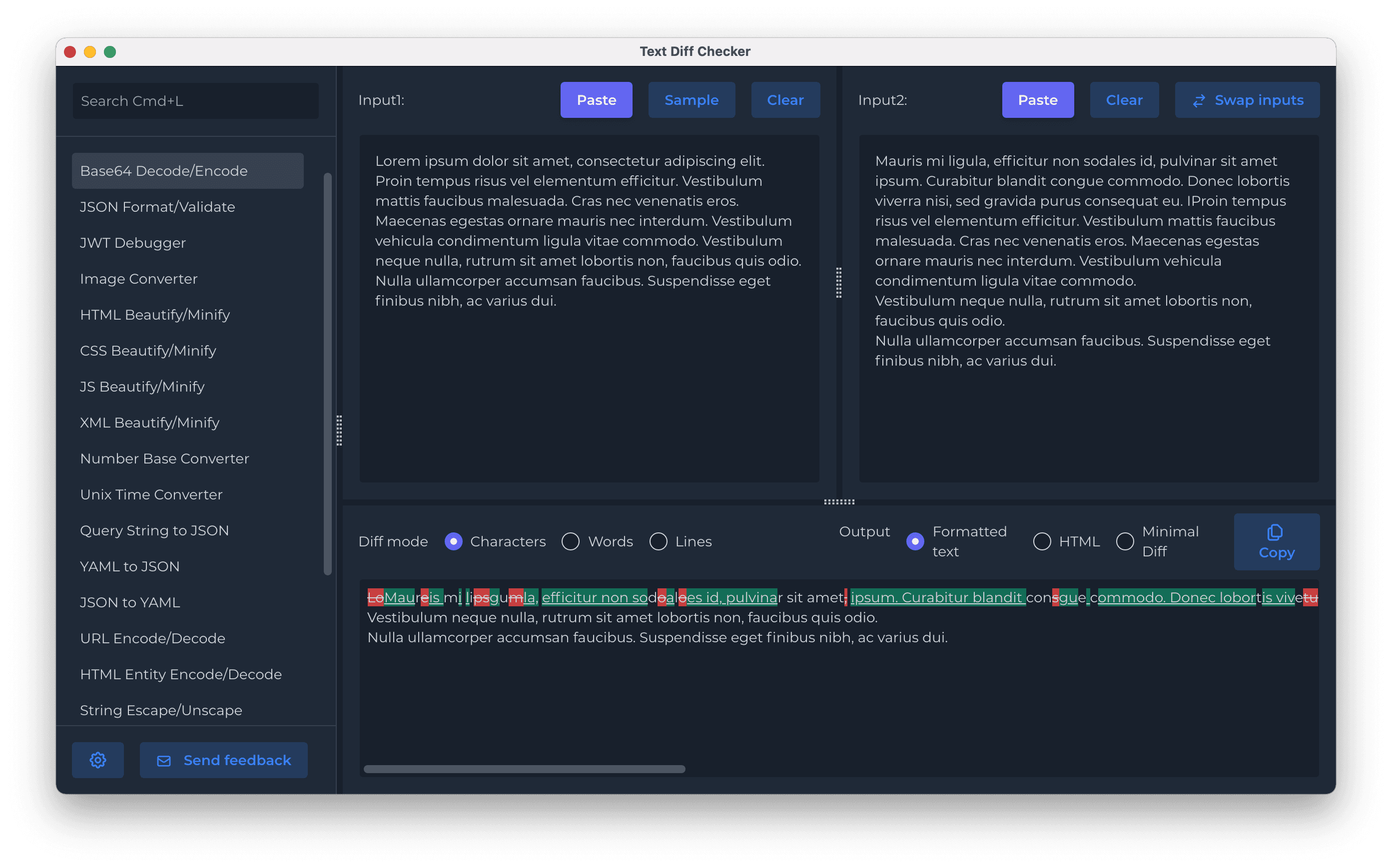
An O(ND) Difference Algorithm and Its Variations

Abstract The problems of finding a longest common subsequence of two sequences A and B and a shortest edit script for transforming A into B have long been known to be dual problems. In this paper, they are shown to be equivalent to finding a shortest/longest path in an edit graph. Using this perspective, a simple O(ND) time and space algorithm is developed where N is the sum of the lengths of A and B and D is the size of the minimum edit script for A and B. The algorithm performs well when differences are small (sequences are similar) and is consequently fast in typical applications. The algorithm is shown to have O(N +D expected-time performance under a basic stochastic model. A refinement of the algorithm requires only O(N) space, and the use of suffix trees leads to an O(NlgN +D ) time variation. More on Wiki

Download for Windows